Algorithme de Widgerson
- Principe de l'algorithme:
L’algorithme de Widgerson est un algorithme de coloration assez spécial, car il n’est applicable que pour les graphes où 3 couleurs sont nécessaires. De plus, il fait appel à deux autres algorithmes de la coloration de graphe. Cet algorithme consiste à trouver tous les sommets avec au moins voisins non coloriés, où n est égal au nombre de sommets du graphe. On applique à ces sommets l’algorithme de ‘2-coloriage’. On va donc utiliser deux couleurs différentes, pour colorier les voisins de ces sommets. Une fois cette étape réalisée, on applique l’algorithme glouton aux sommets restants.
- Analyse de l'algorithme:
L’algorithme Widgerson ne s’applique que pour les algorithmes 3-coloriables. Pour utiliser cet algorithme il faut donc s’assurer préalablement que le graphe à colorier rempli cette condition. Ensuite, il nécessite la connaissance des algorithmes glouton et 2-coloriage, ce qui peut rendre son exécution plus compliquée.
Algorithme Dsatur
- Principe de l'algorithme:
Tout comme l’algorithme de Welsh-Powell, l’algorithme Dsatur utilise un tri des sommets par ordre de degrés décroissants. Son fonctionnement est assez similaire à l’algorithme glouton. Une fois le tri des sommets effectué, on colorie le sommet de degré maximum avec la couleur 1. Ensuite, le prochain sommet à traiter est le sommet avec le plus haut degré de saturation (DSAT, nombre de couleurs différentes utilisées pour colorier ses voisins). Si plusieurs sommets ont le même degré de saturation, celui choisi est celui avec le plus grand nombre de degrés. On associe à ce sommet le plus petit entier possible, et on le colorie en la couleur associée. On répète ce procédé jusqu’à ce que tous les sommets soient coloriés.
- Analyse de l'algorithme:
L’algorithme Dsatur, comme nous l’avons vu précédemment, utilise également un tri des sommets préalable. De la même manière que pour l’algorithme de Welsh-Powell, cette étape peut donc demander du temps. Ensuite, de même que pour l’algorithme glouton, l’algorithme Dsatur est assez simple à exécuter. Concernant, le résultat obtenu, l’algorithme fournit un résultat optimal dans 90% des cas, mais il est possible d’obtenir un mauvais résultat pour certains graphes.
Algorithme glouton
- Principe de l'algorithme:
Un algorithme glouton consiste à résoudre un problème « pas à pas » et de choisir à chaque étape le meilleur choix possible. En coloration de graphe, l’algorithme glouton associe des couleurs à des entiers naturels. Pour chaque sommet, il s’agit de choisir le plus petit entier qui n’appartient pas à l’ensemble des entiers utilisés pour colorier les voisins de ce sommet. On colorie alors le sommet en la couleur associée à l’entier.
- Analsye de l'algorithme:
L'exécution de l'algorithme glouton est plutôt simple et intuitive. Cependant, pour des graphes possédant beaucoup d’arêtes, son exécution peut s’avérer plus longue et compliquée. De plus, il existe des graphes où le résultat obtenu est très loin d’une coloration optimale.
Planning final, bilan et sources
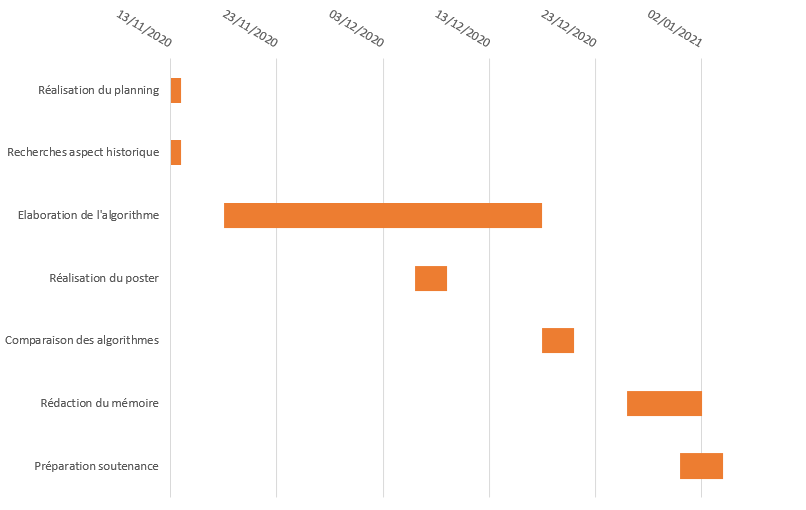
- Planning final:
- Bilan:
Pour colorier un graphe de manière optimale, il existe donc plusieurs méthodes et plusieurs algorithmes bien différents. Nous avons vu aussi qu’aucun des algorithmes étudiés ne présente un résultat parfait dans absolument tous les cas.
Nous avons tenté de réaliser deux algorithmes utilisant deux approches différentes, soit par le tri préalable des sommets, soit depuis un sommet initial. Cependant, nos algorithmes, tout comme les algorithmes existants, ne proposent pas dans tous les cas un résultat optimal. De plus, nos algorithmes élaborés, s’approchent des algorithmes glouton et Welsh-Powell au niveau de leur exécution.
Pour conclure, ce projet nous a permis de voir, qu’il peut être difficile de proposer une solution algorithmique nouvelle et la plus optimale possible, pour la coloration de graphe. Il était néanmoins intéressant d’étudier les différents algorithmes existants, et d’observer les différentes approches et solutions réalisées par leurs auteurs.
- Sources:
|
Sources |
Fiabilité |
|
- Définition des notions mathématiques : Nombre chromatique : https://www.alloprof.qc.ca/fr/eleves/bv/mathematiques/le-nombre-chromatique-m1015 Graphe : https://fr.wikipedia.org/wiki/Th%C3%A9orie_des_graphes#Graphe
|
Grâce aux connaissances acquises l’an dernier en mathématiques, nous avons pu nous assurer de la fiabilité de ces sources. |
|
- Aspect historique : https://cours-info.iut-bm.univ-fcomte.fr/wiki/pmwiki.php/Graphes/TP6bis https://www.researchgate.net/Graph_Coloring_History.pdf https://fr.wikipedia.org/wiki/Coloration_de_graphe#Historique
|
Pour nous assurer de proposer un aspect historique cohérent, nous avons consulté plusieurs sites, en vérifiant la similitude des événements évoqués. |
|
- Etudes des algorithmes : Welsh-Powell : https://fr.wikipedia.org/wiki/Algorithme_de_Welsh_et_Powell Glouton : https://en.wikipedia.org/wiki/Greedy_coloring Dsatur : https://fr.wikipedia.org/wiki/DSATUR Widgerson : https://fr.wikipedia.org/wiki/Algorithme_de_Wigderson
|
Pour l’algorithme de Welsh-Powell, nous avons eu l’occasion de l’étudier l’an dernier en module de mathématiques. Pour les autres algorithmes nous avons consulté plusieurs sites pour nous assurer de la fiabilité de ceux choisis. |
Présentation du sujet
Pour ce projet de modélisations mathématiques, notre sujet est le suivant : Graphes : algorithme de coloration. Nous étudierons la théorie des graphes, et plus particulièrement, la coloration de graphe. Cette coloration de graphe permet d'affecter une couleur à chacun des sommets d'un graphe, tout en faisant en sorte que deux sommets adjacents possèdent une couleur différente.
Nous avons donc pour objectif de créer un algorithme permettant la coloration de graphe.
Nous tenterons de rendre cet algorithme le plus efficace possible, de manière à ce que le nombre de couleurs obtenues soit le plus petit possible.
Nous étudierons aussi l'aspect historique de la coloration de graphe, et comment ce procédé peut être utilisé dans certains domaines.
Enfin, nous analyserons et comparerons les algorithmes deja existants.